Comenzaremos viendo algunas suposiciones:
1) La célula es considerada como un cable homogéneo con dos medios conductores, uno intracelular y otro extracelular, separados por una membrana cuya resistencia y capacitancia están en paralelo.
2) La célula tiene un diámetro mucho menor que su longitud y la resistencia de la membrana es suficientemente alta como para considerar que una sección transversal de pequeña longitud (Δx) es isopotencial.
3) Las resistencias de los medios intra- y extracelular, así como la de la membrana, tienen un comportamiento óhmico (lineal).
Y algunas definiciones:
ii - corriente intracelular (A/cm)
im - corriente transversal (de membrana; A/cm)
cm - capacitancia de membrana en 1 cm de longitud de célula (cm = Cm 2 π a; F/cm)
Cm - capacitancia de 1 cm2 de membrana (F/cm2)
ri - resistencia longitudinal de 1 cm de célula (ri = Ri / π a2; Ω/cm)
Ri - resistividad del axoplasma (Ω·cm)
rm - resistencia de membrana en 1 cm de longitud de célula (rm = Rm / 2 π a; Ω·cm)
Rm - resistividad de 1 cm2 de membrana (Ω·cm2)
i o - corriente inyectada como un pulso cuadrado en x = 0 (A)
Vo - cambio en el potencial transmembrana (interior menos exterior) en x = 0 como consecuencia de i o
Vx - cambio en el potencial transmembrana en un punto x, como consecuencia de i o
DERIVACIONES DE UN CABLE INFINITAMENTE LARGO
Representación esquemática de una membrana celular como un cable unidimensional de longitud infinita.
Inicialmente inyectamos una corriente Io en un lugar del cable y nos preguntamos cómo cambia la corriente interna conforme nos alejamos del punto de inyección. En la Figura 1 se puede observar que la corriente inyectada intracelularmente (Io) se divide en la que va hacia la derecha y la que va hacia la izquierda del punto de inyección. Tomando una dirección cualquiera, por ejemplo la que va hacia la derecha, la diferencia entre la corriente ii en un segmento dx (Figura 2) y el siguiente, será aquella que se pierde porque sale a través de la membrana.
Esto puede describirse con la siguiente ecuación:
Esta ecuación indica que cuando la distancia aumenta (+ dx), la corriente i i disminuye (-di i), ya que una fracción (i m) de la corriente escapa a través de la membrana en cada incremento dx.
Re-arreglando la ecuación (1) tenemos,
Otra ecuación que podemos derivar fácilmente es aquella que responde a la pregunta, ¿Cómo cambia el voltaje de un segmento dx con respecto al voltaje en el segmento contiguo? De nuevo, analizando el circuito vemos que la diferencia en el voltaje entre los dos segmentos será debida a la caída de voltaje a través de la resistencia longitudinal (r i).
Esto puede expresarse con la siguiente ecuación,
Esta ecuación indica que conforme la distancia aumenta (dx) el potencial transmembrana disminuye (-dVx) por una cantidad igual a la caída de voltaje (ri ii) en la resistencia ri.
Despejando ii en la ecuación (3) obtenemos,
Ahora, consideremos un solo segmento dx de un cable infinitamente largo como el ilustrado en la Figura 2.
Figura 2. Segmento (dx) de un cable infinitamente largo.
En el circuito de la Figura 2 se observa que la corriente total cruzando la membrana es igual a la suma de las corrientes que fluyen a través de la resistencia y el capacitor.
sustituyendo las corrientes resistivas y capacitivas en la ecuación (5) por sus equivalentes de acuerdo a la ley de Ohm, tenemos,
A partir de las ecuaciones (2) y (6) también obtenemos:
Aquí hemos introducido el operador " ∂ " para indicar que Vx es una función no solamente de la distancia sino también del tiempo. Ahora, diferenciando la ecuación (4) con respecto a x y sustituyendo en la ecuación (7), tenemos,
y multiplicando ambos lados de la ecuación (8) por rm obtenemos,
y definimos los siguientes parámetros,
donde τ m es la constante de tiempo del circuito en el que la resistencia y la capacitancia se encuentran en paralelo (R || C) y que representa a un segmento del cable. Este parámetro mide el tiemo que tarda un cambio de voltaje en alcanzar la fracción e de su valor final (ver la sección X). El significado físico de λ2 será analizado posteriormente.
Finalmente, la sustitución de las ecuaciones (10) y (11) en la ecuación (9) produce,
Esta ecuación (12) es la "ecuación general del cable" e integrándola se puede obtener el potencial de membrana como función del tiempo y la distancia a lo largo del cable.
ólo pueden generar fuerzas interiores, cuya
intensidad y dirección depe
nderán de las cargas que
actúan en el sistema
Referencias:
Brazier, M.A.B. 1984. A History of Neurophysiology in the 17th & 18th Centuries. Raven Press. New York.
Brazier, M.A.B. 1988. A History of Neurophysiology in the 19th Century. Raven Press. New York.
Davis, L., and R. Lorente de Nó. 1947. Contribution to the mathematical theory of the electrotonus. Studies from the Rockefeller Institute. Vol. 131. Rockefeller Institute, New York. Chp IX.
Dibner, B. 1964. The Atlantic Cable. Ginn (Blaisdell). New York
Hermann, L. 1879a. Allgemeine Muskelphysic. En: Handbuch der Physiologie. Leipzig, F.C.W. Vogel. 1, pt 1,3.
http://www.facmed.unam.mx/Libro-NeuroFisio/04-NeuroFisioCelular/Cable/Cable-Ecuaciones.html






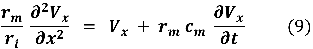




Comentarios
Publicar un comentario